티어 – 골드 4
알고리즘 분류
- 구현
- 브루트포스
- 백트래킹
문제
크기가 N×M 크기인 배열 A가 있을때, 배열 A의 값은 각 행에 있는 모든 수의 합 중 최솟값을 의미한다. 배열 A가 아래와 같은 경우 1행의 합은 6, 2행의 합은 4, 3행의 합은 15이다. 따라서, 배열 A의 값은 4이다.
1 2 3
2 1 1
4 5 6배열은 회전 연산을 수행할 수 있다. 회전 연산은 세 정수 (r, c, s)로 이루어져 있고, 가장 왼쪽 윗 칸이 (r-s, c-s), 가장 오른쪽 아랫 칸이 (r+s, c+s)인 정사각형을 시계 방향으로 한 칸씩 돌린다는 의미이다. 배열의 칸 (r, c)는 r행 c열을 의미한다.
예를 들어, 배열 A의 크기가 6×6이고, 회전 연산이 (3, 4, 2)인 경우에는 아래 그림과 같이 회전하게 된다.

회전 연산이 두 개 이상이면, 연산을 수행한 순서에 따라 최종 배열이 다르다.
다음은 배열 A의 크기가 5×6이고, 회전 연산이 (3, 4, 2), (4, 2, 1)인 경우의 예시이다.
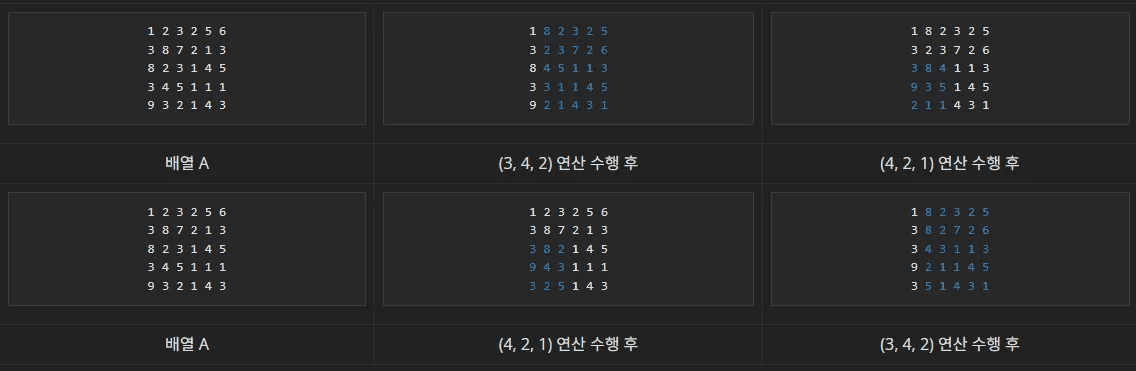
배열 A에 (3, 4, 2), (4, 2, 1) 순서로 연산을 수행하면 배열 A의 값은 12, (4, 2, 1), (3, 4, 2) 순서로 연산을 수행하면 15 이다.
배열 A와 사용 가능한 회전 연산이 주어졌을 때, 배열 A의 값의 최솟값을 구해보자. 회전 연산은 모두 한 번씩 사용해야 하며, 순서는 임의로 정해도 된다.
문제 접근 방식
- map을 입력받는다.
- 회전 연산 정보를 입력받고 저장한다.
- 회전 연산의 순서를 바꾸어 적용해야 하므로 회전 연산 정보의 순열을 구한다.
- 구한 순열마다 원본 배열을 복사한 뒤, 순서대로 회전 연산을 수행한다.
- 모든 연산을 수행한 후 각 행의 합을 계산하여 그 중 최솟값을 갱신한다.
구현 코드
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
static int[][] map;
static int[][] roArr;
static List<Integer[][]> roPerm = new ArrayList<>();
static int minResult = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int k = sc.nextInt();
// map 입력
int[][] originMap = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
originMap[i][j] = sc.nextInt();
}
}
// 회전 연산 정보 저장
roArr = new int[k][3];
for (int i = 0; i < k; i++) {
roArr[i][0] = sc.nextInt();
roArr[i][1] = sc.nextInt();
roArr[i][2] = sc.nextInt();
}
// 회전 연산 정보 순열 구하기
perm(0, new int[k][3], new boolean[k]);
for (Integer[][] roInfos : roPerm) {
// 이동시킬 맵 복사
map = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
map[i][j] = originMap[i][j];
}
}
// 회전 연산 정보 불러오기
for (int i = 0; i < k; i++) {
int top = roInfos[i][0] - roInfos[i][2] - 1;
int left = roInfos[i][1] - roInfos[i][2] - 1;
int bottom = roInfos[i][0] + roInfos[i][2] - 1;
int right = roInfos[i][1] + roInfos[i][2] - 1;
int pre = map[bottom][left];
int layerCount = Math.min(bottom - top, right - left) / 2;
// 한 레이어씩 돌리기
for (int l = 0; l < layerCount; l++) {
int temp;
// 배열 한 바퀴 돌리기
for (int q = bottom; q > top; q--) { // 아래에서 위로
temp = map[q][left];
map[q][left] = pre;
pre = temp;
}
for (int q = left; q < right; q++) { // 왼쪽에서 오른쪽
temp = map[top][q];
map[top][q] = pre;
pre = temp;
}
for (int q = top; q < bottom; q++) { // 위에서 아래로
temp = map[q][right];
map[q][right] = pre;
pre = temp;
}
for (int q = right; q > left; q--) { // 오른쪽에서 왼쪽
temp = map[bottom][q];
map[bottom][q] = pre;
pre = temp;
}
map[bottom][left] = pre;
// 안쪽 레이어로 이동
top++;
left++;
bottom--;
right--;
}
}
// 각 행의 합 계산 후 최소값 갱신
for (int q = 0; q < n; q++) {
int temp = 0;
for (int p = 0; p < m; p++) {
temp += map[q][p];
}
if (temp < minResult) {
minResult = temp;
}
}
}
System.out.println(minResult);
}
static void perm(int depth, int[][] sel, boolean[] v) {
// basis: 모든 회전 연산을 선택한 경우
if (depth == roArr.length) {
Integer[][] temp = new Integer[roArr.length][3];
for (int i = 0; i < roArr.length; i++) {
for (int j = 0; j < 3; j++) {
temp[i][j] = sel[i][j];
}
}
roPerm.add(temp);
return;
}
// inductive: 아직 사용하지 않은 회전 연산을 선택
for (int i = 0; i < roArr.length; i++) {
if (!v[i]) {
v[i] = true;
sel[depth] = roArr[i];
perm(depth + 1, sel, v);
v[i] = false;
}
}
}
}풀이 과정 상세 설명
- 입력 및 초기화
Scanner를 이용하여 배열의 크기 N, M과 회전 연산의 개수 K를 입력받는다.
originMap을 입력받고 저장한다.
roArr 배열에 저장한다.
- 순열 생성 (백트래킹)
perm 메소드를 활용하여 사용 가능한 회전 연산의 모든 순서를 roPerm 리스트에 저장한다.
- 회전 연산 수행
map에 복사한다.
- 최소 행 합 계산
minResult에 갱신한다.
- 결과 출력
마치며 (결론)
문제의 핵심은 회전 연산의 순서를 어떻게 적용하느냐에 있다.
모든 순열을 고려하여 각 경우마다 회전 연산을 시뮬레이션하는 방식으로 해결하였다.
이 문제를 통해 브루트포스와 백트래킹 기법을 활용한 문제 해결법을 익힐 수 있었다.
배열 회전 관련 문제는 이걸로 끝 조금 더 필요하다면 추가로 배열 돌리기 5까지 추천한다.